نظریه گرانش حرکتی و اثبات کامل آن بر اساس نظریه نسبیت عمومی

نظریه گرانش حرکتی و اثبات کامل آن بر اساس نظریه نسبیت عمومی

بر اساس دیدگاه گرانشی موجود در نظریه نسبیت عمومی اینشتین به عنوان مثال خورشید با تاثیر بر بافت فضا و زمان پیرامون خود موجب وارد شدن نیروی شتاب گرانشی بر زمین و در نتیجه شناور ماندن حرکت زمین در مدار خود به دور خورشید می شود پس اگر فرض کنیم که در یک لحظه خورشید به طور کامل ناپدید شود بر اساس دیدگاه گرانشی نیوتن زمین هم در همان لحظه ناپدید شدن خورشید از اثرات عدم وجود گرانشی خورشید متاثر شده و در نتیجه زمین بلافاصله از مدار خود منحرف شده و خارج می گردد ولی بر اساس دیدگاه گرانشی نسبیت عمومی اینشتین که در حال حاضر آزمایشات و مشاهدات بسیاری آن را تایید می کنند به دلیل اینکه نیروی گرانش خورشید نسبت به زمین را حاصل وجود امواجی گرانشی از سوی خورشید که با سرعتی تقریبا برابر با سرعت نور در خلاء و تاثیرگذاری آن بر بافت فضا و زمان معرفی می کند در نتیجه از زمان ناپدید شدن خورشید تا زمان تاثیر محو شدن اثر نیروی حاصل از شتاب گرانشی خورشید بر زمین تقریبا کمی بیش از هشت دقیقه که برابر با زمان رسیدن نور خورشید به زمین می باشد، طول خواهد کشید. با توجه به مطالب مطرح شده در مورد دیدگاه های نیوتن و اینشتین پیرامون مبحث گرانش ، نظریه ای جدید با نام نظریه گرانش حرکتی شکل می گیرد که این نظریه با درست دانستن پایه و بنیاد معادله گرانش عمومی نیوتن و نیز وجود امواج گرانشی پیش بینی شده توسط اینشتین ، دیدگاه و معادلات جدید و کامل تری را جهت محاسبه نیروی حاصل از شتاب گرانشی معرفی کرده و توسط آنها به بسیاری از سئوالات و ابهامات مطرح شده در کیهان شناسی پاسخ داده و پیش بینی هایی را هم در این حوزه ارائه می کند.

توصیف نظریه گرانش حرکتی:

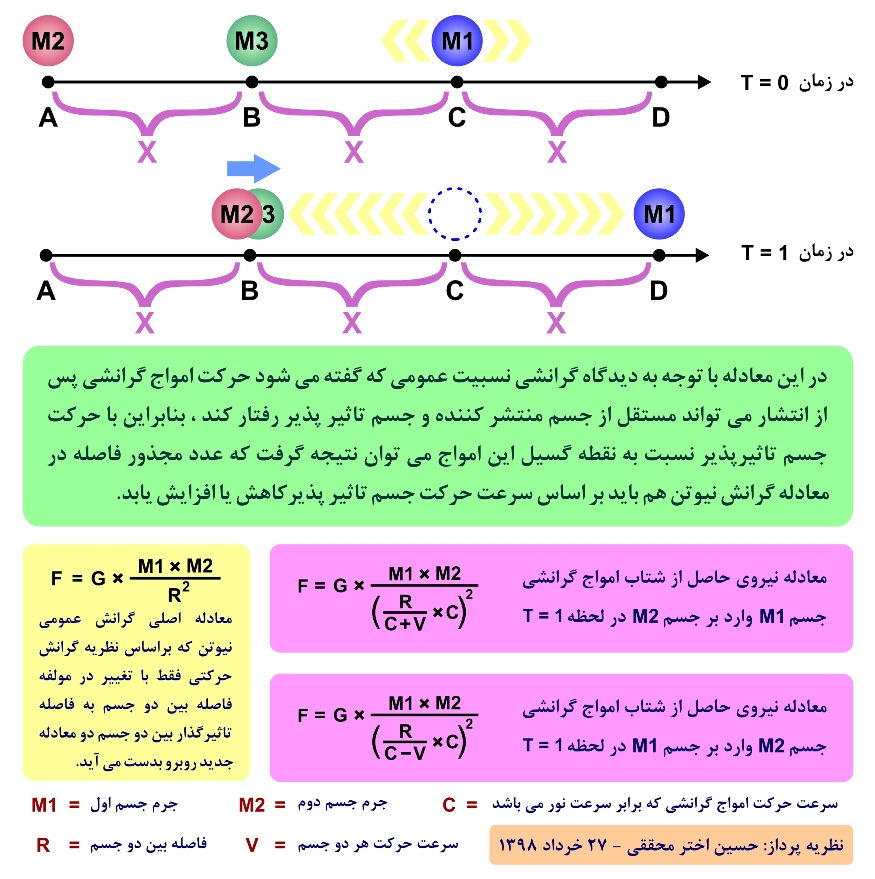
همان طور که در شکل زیر مشاهده می کنید اگر ما چهار نقطهA  و B و C و D  بر روی یک خط مستقیم در فضا داشته باشیم به طوری که فاصله هر یک از این نقاط کنار هم به طور مثال برابر با سیصد میلیون متر یا به عبارتی برابر با X یا همان مسافتی که نور در یک ثانیه می تواند در خلاء طی کند باشد و همچنین اجسامی بسیار متراکم و پر جرم با جرمی برابر با یکدیگر و با نام های M1 و M2 و M3 داشته باشیم که به ترتیب M1 روی نقطه C و M2 روی نقطه A و M3 روی نقطه B قرار گرفته باشند در نتیجه بدون در نظر گرفتن اثرات نیروی گرانشی بین دو جسم M2 و M3 نسبت به یکدیگر خواهیم دید که بر اساس دیدگاه گرانشی نسبیت عمومی در زمان T = 0 موجی گرانشی از جسم M1 که در زمان T = 0 در نقطه C قرار دارد در فضا منتشر شده و این موج تا رسیدنش به نقطه B باید مسافتی برابر با X یا به عبارتی در حدود سیصد میلیون متر را تا زمان T = 1 یعنی معادل یک ثانیه بپیماید و بر فضا و زمان پیرامون نقطه B تاثیر گذاشته و در نتیجه مقداری نیروی شتاب گرانشی با نام F3 را بر جسم M3 وارد کند و همچنین این موج گرانشی تا رسیدن به نقطه A باید مسافتی برابر با 2*X یا به عبارتی در حدود ششصد میلیون متر را تا زمان T = 2 یعنی معادل دو ثانیه از لحظه انتشار در فضا بپیماید و بر فضا و زمان پیرامون نقطه A تاثیر گذاشته و در نتیجه نیروی شتاب گرانشی بسیار کمتری نسبت به نیروی شتاب گرانشی F3 با نام F2 را بر جسم M2 وارد کند.

تا اینجای کار همه چیز طبیعی پیش می رود ولی اگر فرض کنیم که در فاصله زمانی T = 0 تا T = 1 که موج گرانشی از نقطه C به سمت نقطه B پیش می رود جسم M1 هم با همان سرعت انتشار امواج گرانشی از نقطه C به سمت نقطه D حرکت کند و در نتیجه پس از حدود یک ثانیه یعنی زمانی که امواج گرانشی به نقطه B رسیده اند جسم M1 هم به نقطه D می رسد که با توجه به دیدگاه گرانشی نظریه نسبیت اینشتین در لحظه T = 1 باز هم مانند زمانی که جسم M1 در همان نقطه C ثابت مانده بود شتاب گرانشی وارد بر جسم M3 به دلیل انحنای معینی که این امواج گرانشی بر ساختار فضا و زمان پیرامون نقطه B ایجاد می کنند ثابت می باشد و یعنی حرکت جسم M1 پس از گسیل امواج گرانشی در فضا تاثیری بر کیفیت آن امواج نمی گذارد و این امواج به طور مستقل رفتار می کنند ولی نکته اصلی هم همین است که حالا اگر همزمان با اینکه جسم M1 از نقطه C به نقطه D حرکت می کند جسم M2 هم با همان سرعت امواج گرانشی از نقطه A به نقطه B حرکت کند و بنابراین بعد از گذشت یک ثانیه و در زمان T = 1 جسم M1 به نقطه D و جسم M2 به نقطه B و همچنین امواج گرانشی هم به نقطه B رسیده اند و در نتیجه جسم M2 مانند جسم M3 اثرات گرانشی یکسانی را که توسط گسیل امواج گرانشی حاصل از جسم M1 ایجاد شده است را با نام نیروی شتاب گرانشی F3 دریافت خواهد کرد و نکته مهمتر این است که فاصله دو جسم M1 و M2 همچنان یکسان است و در هر دو زمان T = 0 و T = 1 فاصله بین آنها برابر با 2*X یعنی معادل ششصد میلیون متر است در حالی که در این حالت یعنی حالتی که دو جسم M1 و M2 در یک راستا حرکت می کنند جسم M2 نیروی شتاب گرانشی بیشتری با نام F3 را از جسم M1 دریافت می کند در حالی که در صورت ساکن بودن دو جسم M1 و M2 این نیروی شتاب گرانشی به نیروی شتاب گرانشی کمتری با نام F2 کاهش پیدا می کرد.

بنابراین با حرکت دو جسم با یک سرعت و در یک راستا و با حفظ فاصله بین دو جسم نسبت به حالت سکون آنها مشاهده می کنیم که نیروی تاثیرگذار شتاب گرانشی جسم جلوتر نسبت به جسم عقب تر یعنی جسم M1 بر جسم M2 افزایش می یابد و جالب تر این نکته است که بر اساس دیدگاه گرانشی نظریه نسبیت عمومی اینشتین چون امواج گرانشی با انحنای فضا و زمان موجب پدیدار آمدن شتاب گرانشی در اجسام می شوند در نتیجه باید انتظار داشت که به صورت متقابل هم نیروی تاثیرگذار شتاب گرانشی جسم عقب تر نسبت به جسم جلوتر یعنی جسم M2 بر جسم M1 کاهش یابد.

در اینجا ما فرض کردیم که سرعت حرکت هر دو جسم M1 و M2 برابر با سرعت حرکت امواج گرانشی و به عبارتی برابر با سرعت نور است که رسیدن به چنین سرعتی محال است ولی باید در نظر داشت که این فقط یک فرض است و چنین پدیده ای یعنی تغییر توازن تاثیر گرانشی اجسام در حال حرکت نسبت به اجسام در حال سکون حتی با سرعت های کمتر از سرعت نور هم به وجود می آید و فقط کافی است که حرکت دو جسم M1 و M2 به طور پیوسته ادامه داشته باشد و بر این اساس مطابق با شکل زیر معادلات گرانش عمومی نیوتن بر اساس این نظریه با کمی اصلاحات جزئی تصحیح می شود.

توصیف معادله اصلاح شده گرانش عمومی نیوتن بر اساس نظریه گرانش حرکتی:

با توجه با معادله گرانش عمومی نیوتن مولفه F برابر با نیروی حاصل از شتاب گرانشی وارد بر هر دو جسم M1 و M2 بوده که برای هر دو جسم یکسان می باشد و مولفه G برابر با ثابت جهانی گرانش نیوتن و M1 جرم جسم اول و M2 جرم جسم دوم و R هم برابر با فاصله بین دو جسم M1 و M2 می باشد.

در حالت سکون دو جسم M1 و M2 قانون گرانش عمومی نیوتن بدون هیچ اصلاحی به درستی کار می کند و صحیح است ولی در زمانی که حداقل یکی از دو جسم M1 و M2 شروع به حرکت کرده و به خصوص سرعت بالایی هم داشته باشند معادله گرانش عمومی نیوتن دچار مقداری انحراف در محاسبات به دست آمده نسبت به مشاهدات می شود و دلیل اصلی آن هم این نکته است که معادله گرانش عمومی نیوتن سرعت تاثیرگذاری نیروی گرانش را بینهایت و به عبارتی آنی و لحظه ای بیان می کند و در نتیجه حرکت حداقل یکی از دو جسم M1 و M2 هم نباید تغییری در نیروی حاصل از شتاب گرانشی ایجاد کند که البته در دیدگاه اینشتین و نیز مشاهدات نجومی امروزی و بسیاری از مستندات دیگر این قضیه یعنی تاثیر آنی و لحظه ای نیروی گرانش به طور کامل رد شده و برای سرعت حرکت امواج گرانشی سرعتی مشخص و در محدوده سرعت حرکت نور در خلاء در نظر گرفته می شود که بنا بر همین اصل در نظریه گرانش حرکتی ، سرعت حرکت اجسام M1 و M2  وارد معادله اصلی گرانش عمومی نیوتن شده و دو معادله مختلف را با توجه به وضعیت تقدم حرکتی هر یک از دو جسم نسبت به یکدیگر ارائه می دهد که در این دو معادله علاوه بر مولفه های قبلی موجود در معادله اصلی گرانش عمومی نیوتن ، دو مولفه دیگر به نام V که سرعت ثابت حرکت اجسام M1 و M2  و نیز مولفه C که همان سرعت حرکت امواج گرانشی در فضا که تقریبا برابر با سرعت حرکت نور در خلاء می باشد اضافه شده است در این دو معادله جدید می خواهیم بدانیم که مقدار مسافت طی شده توسط جسم مورد هدف یا همان جسم تاثیر پذیر از گرانش ، تا زمان رسیدن امواج گرانشی به فضای پیرامون آن چقدر خواهد بود که در این دو معادله تنها تفاوت ، وجود یک علامت مثبت یا منفی در معادله است که انتخاب این علامت با توجه به وضعیت قرارگیری هر یک از اجسام نسبت به جسم دیگر که در راستای حرکت هر دو جسم در جلو یا عقب جسم دیگر قرار دارد تعیین می شود.

در این دو معادله اگر با توجه به راستای حرکتی هر دو جسم ، جسم مورد هدف ( جسم تاثیر پذیر از نیروی شتاب گرانشی ) که در معادله اول جسم M2 است به سمت امواج گرانشی منتشر شده از جسم دیگر که در اینجا جسم M1 است حرکت کند در این صورت علامت مورد نظر مثبت و اگر جسم مورد هدف ( جسم تاثیر پذیر از نیروی شتاب گرانشی ) که در معادله دوم جسم M1 است از امواج گرانشی منتشر شده از جسم دیگر که در اینجا جسم M2 است دور شود در این صورت علامت مورد نظر منفی خواهد بود. با توجه به سرعت فرضی حاصل از برآیند سرعت امواج گرانشی و سرعت حرکت جسم ، اگر مسافت قابل مشاهده بین دو جسم یعنی R را بر این سرعت فرضی حاصله تقسیم کنیم در این صورت مدت زمان لازم برای رسیدن امواج گرانشی از لحظه انتشار تا لحظه رسیدن به فضای پیرامون جسم مورد هدف بدست آمده و در نتیجه اگر این زمان در سرعت واقعی حرکت امواج گرانشی یعنی C ضرب شود مقدار R تاثیرگذار و یا به عبارتی مسافت برآیند حاصل از حرکت جسم و حرکت امواج گرانشی بدست می آید که برای اجسام در حال حرکت ، مقدار نیروی حاصل از شتاب گرانشی به جای مولفه R  قابل مشاهده به مولفه R تاثیرگذار بستگی دارد. همچنین لازم به ذکر است که در این معادله سرعت حرکت امواج گرانشی به طور فرض برابر سرعت حرکت نور در خلاء بیان شده که لازم است مقدار واقعی آن دقیقا محاسبه شود.
نظریه پرداز: حسین اختر محققی - 27 خرداد 1398
جهت دانلود مقاله روی همین لینک کلیک کنید

توصیف چرایی تغییر تاثیر نیروی گرانش در نظریه گرانش حرکتی با دو مثال ساده

فرض کنید که سیاره مریخ از نظر حجم و جرم دقیقا شبیه به زمین بوده و فاصله اش با خورشید هم دو برابر فاصله زمین تا خورشید باشد و فرض کنید که نیروی حاصل از گرانش خورشید بر زمین به عنوان مثال فرضا 20 واحد فرضی می باشد پس نیروی حاصل از گرانش خورشید بر مریخ که فاصله اش تا خورشید دو برابر فاصله زمین تا خورشید است بسیار کمتر و به طور فرض 10 واحد فرضی می باشد. ( البته این مقدار دقیق نیست و فقط به منظور نشان دادن کمتر بودن آن نسبت به گرانش وارد بر زمین بیان شده است ) حالا فرض می کنیم که خورشید تا مدتی وجود نداشته و در یک لحظه ظاهر می شود پس با توجه به نظریه نسبیت عمومی اینشتین ، موج گرانشی حاصل از ظاهر شدن خورشید در حدود 8 دقیقه طول می کشد تا به زمین و دو برابر آن مدت یعنی در حدود 16 دقیقه طول می کشد تا به مریخ برسد. تا اینجای کار اتفاق خاصی رخ نمی دهد و نتایج آزمایشات و همه محاسبات این قضیه را تایید می کنند. ولی سئوال این است که اگر در زمانی که خورشید به یکباره ظاهر می شود و شروع به انتشار موجی گرانشی می کند در همین لحظه هم مریخ با سرعت نور ( که البته این سرعت بعید است و فقط برای راحتی نتیجه گیری این سرعت بیان شده است و سرعت های کمتر از آن هم مورد تایید است ) به سمت خورشید حرکت کرده و در لحظه ای که موج گرانشی خورشید مطابق نظریه نسبیت عمومی بر فضا و زمان پیرامون زمین تاثیر گذاشته و نیروی حاصل از گرانش 20 واحدی را بر زمین وارد می کند سیاره مریخ هم به همین جایگاه مداری زمین یعنی فاصله ای برابر با فاصله زمین تا خورشید رسیده و همچنان با همان سرعت قبل هم در حال حرکت باشد بنابراین به طور منطقی باید نیروی حاصل از گرانش خورشید به مریخ هم در این نقطه از فضا برابر با همان نیروی 20 واحدی وارد بر زمین باشد. حالا در ادامه فرض می کنیم که خورشید به محض ظاهر شدن و شروع به انتشار موج گرانشی ، با همان سرعتی که مریخ به خورشید نزدیک می شود از مریخ دور شود ولی همچنان به انتشار گرانش ادامه می دهد بنابراین در لحظه ای که مریخ به نقطه جایگاه زمین رسیده است خورشید هم به همان میزان مسافت طی شده از مریخ دور شده است و در نتیجه فاصله بین خورشید و مریخ همچنان یکسان بوده ولی مریخ نیروی حاصل از گرانش بیشتری یعنی نیروی حاصل از گرانش 20 واحدی را از سوی خورشید دریافت می کند در حالی که با ساکن بودن خورشید و مریخ و با حفظ همان فاصله ، مریخ نیروی حاصل از گرانش کمتری یعنی نیروی حاصل از گرانش 10 واحدی را از سوی خورشید دریافت می کرد پس نتیجه می گیریم که با استمرار این کار یعنی حرکت مریخ و خورشید در یک راستا و با سرعتی ثابت ، نیروی حاصل از گرانش خورشید به مریخ بدون هیچگونه تغییری در فاصله بین آنها افزایش می یابد که این قضیه شبیه به دو اتومبیلی است که با یک فاصله ثابت از یکدیگر حرکت کرده و در یک لحظه چرخ اتومبیل جلویی وارد یک چاله آب شده و قطرات آب را به هوا پرتاب می کند که در اینجا اگر سرعت هر دو اتومبیل کم باشد قطرات آب کمی به اتومبیل عقب تر برخورد می کند ولی اگر سرعت دو اتومبیل زیاد باشد قطرات آب بیشتری به اتومبیل عقب تر برخورد می کند. شاید بتوان گفت که گرانش ، اثر کمتری را بر روی اجسام در حال حرکت می گذارد پس در این صورت می توان گفت اگر در همان نقطه موعود که گرانش اثر کمتری را بر روی جسم در حال حرکت می گذارد آن جسم ساکن شده و حرکت نکند پس در نتیجه باید در یک لحظه تاثیر نیروی گرانش بر جسم افزایش یابد پس در این حالت هم دوباره نتیجه خواهیم گرفت که تاثیر نیروی گرانش بر اجسام در حال حرکت نسبت به اجسام ساکن متفاوت خواهد بود و فقط نظریه گرانش حرکتی این بار به صورت معکوس شکل خواهد گرفت و در نتیجه اساس نظریه گرانش حرکتی یعنی تغییر توازن گرانشی برای اجسام در حال حرکت مجددا تایید می شود.

جهت دانلود مقاله روی همین لینک کلیک کنید

چرایی تشکیل ساختار موجی شکل در کهکشان ها بر اساس نظریه گرانش حرکتی

اگر به ساختار کهکشان های بیضوی و مارپیچی توجه کنیم در همه آنها الگویی موجی شکل را مشاهده می کنیم و البته نظریه های گوناگونی در این رابطه و توضیح چگونگی تشکیل این الگوهای موجی شکل در کهکشان ها مطرح شده است که در هر صورت نظریه گرانش حرکتی به سادگی دلیل شکل گیری چنین الگویی را توضیح می دهد. بر اساس نظریه گرانش حرکتی ، اگر یک ستاره را مانند شمعی روشن و عامل گرانش و یا به عبارتی موج گرانشی حاصل از جسم مورد نظر را مانند شعله آن شمع در نظر بگیریم بنابراین چنین شعله ای بعد از پدید آمدن می تواند مستقل از شمع رفتار کند و در این صورت با حرکت دادن شمع مشاهده می کنیم که شعله شمع در سمت مخالف جهت حرکت شمع ، تجمع بیشتری خواهد داشت و حتی اگر همزمان شمع خاموشی در پشت آن شمع حرکت کند ممکن است توسط شعله شمع جلوتر روشن شود بنابراین می توان گفت زمانی که شمع روشن حرکت داده می شود ، در جهت خلاف حرکتش و به فاصله کوتاهی از آن ، آثار و ردپایی از شعله اش باقی خواهد ماند و به عبارتی قدرت تاثیر آن شعله بر خلاف جهت حرکت شمع افزایش خواهد یافت که این قضیه دقیقا شبیه به اصل موجود در نظریه گرانش حرکتی می باشد و حالا اگر تعداد زیادی شمع در الگویی دایره ای و پشت سر هم قرار گرفته و همگی در یک جهت حرکت کنند در این صورت شعله ای حلقه ای را تشکیل خواهند داد که در این حلقه دیگر فضایی خالی بین شعله ها وجود نخواهد داشت و با نزدیک کردن یک شمع جدید به داخل این حلقه به راحتی می توان آن را روشن کرد ولی اگر این ساختار دایره ای شمع ها حرکتی نداشته باشد به دلیل وجود فضای خالی در بین شعله شمع ها ، احتمال روشن شدن شمع مورد نظر کمتر می شود که مشابه چنین شرایطی در مورد تاثیر گرانش ستارگان موجود در کهکشان های بیضوی و تا حدودی در مورد کهکشان های مارپیچی هم اتفاق می افتد و به عنوان مثال به دلیل حرکت ستارگان در کهکشان های بیضوی ، تعداد زیادی حلقه گرانشی در ساختار آنها شکل می گیرد که در این حلقه های گرانشی احتمال فرار ستارگان و گازهای کیهانی بسیار کمتر از فضای خارج از آنها می باشد و با ورود هر چه بیشتر گازها و ستارگان به داخل این حلقه ها ، قدرت پوشش گرانشی حلقه ها افزایش پیدا کرده و بلعکس میزان گازها و اجرام خارج از حلقه ها هم روندی کاهشی را طی می کند و در نتیجه ما ساختار کهکشان های بیضوی را به صورت الگویی موجی حلقه ای و نیز کهکشان های مارپیچی را به صورت الگویی موجی مارپیچی مشاهده می کنیم.
جهت دانلود مقاله روی همین لینک کلیک کنید

پیشنهاد یک آزمایش جهت اثبات پدیده چرخش خودکار کهکشان ها و سیاهچاله ها

پیشنهاد می شود جهت اثبات پدیده چرخش خودکار کهکشان ها و سیاهچاله ها ،  نمونه ای بسیار کوچک و تا حدودی شبیه به یک حلقه از یک کهکشان بیضوی طراحی شود و بدین منظور لوله ای فلزی و توپر با سطح مقطع دایره ای یا بیضی شکل به ضخامت مناسب 10 تا 100 سانتی متر را به صورت حلقه ای دایره ای شکل با قطر مناسب مثلا 10 تا 100 متری تبدیل کرده و آن را در محفظه ای بسیار بزرگ و ایزوله در فضا به طوری که عوامل خارجی نظیر ذرات سرگردان فضایی و غیره تاثیری بر نتایج نداشته باشند قرار داده و سپس حلقه مورد نظر را با سرعتی زیاد به چرخش درآورده و در یک بازه زمانی قابل قبول و تقریبا طولانی ، تغییرات جزئی سرعت چرخش حلقه را با دقتی بسیار زیاد اندازه گیری نمود چون بر اساس نظریه گرانش حرکتی پیش بینی می شود که این حلقه در حال چرخش مانند اصول اولیه چرخش کهکشان های بیضوی و سیاهچاله های چرخان عمل کرده و بنابراین سرعت چرخش آن در یک بازه زمانی طولانی مدت به صورت بسیار جزئی افزایش می یابد و در نتیجه می توان در این آزمایش تاثیر پدیده گرانش حرکتی و یا به عبارتی تغییر توازن گرانش اجسام در حال حرکت نسبت به یکدیگر را مشاهده نمود.
جهت دانلود مقاله روی همین لینک کلیک کنید

لزوم تغییر جزئی در مقدار ثابت جهانی گرانش

با توجه به اینکه زمین بر اساس چرخش به دور خود و گردش به دور خورشید و گردش خورشید در کهکشان و نیز حرکت کهکشان در فضا ، حرکت های مختلفی را تجربه می کند بنابراین اندازه گیری های مختلفی هم که برای بدست آوردن عدد ثابت جهانی گرانش صورت می گیرد تا حدودی تحت تاثیر پدیده گرانش حرکتی قرار گرفته و تاثیری بسیار جزئی در مقادیر آن ایجاد می کند. البته باید توجه داشت که این تاثیر بسیار جزئی است و به راحتی نمی توان آن را مشاهده نمود ولی در ابعاد وسیع قابل مشاهده است و این قضیه شبیه به تاثیر گرانش ماه بر زمین است که هیچگونه اختلالی بر کارکرد ترازوهای معمولی آزمایشگاهی نداشته ولی در ابعاد وسیع می تواند بر آب دریاها و اقیانوس ها اثر گذاشته و موجب تشکیل پدیده مد آب دریاها و اقیانوس ها شود.
جهت دانلود مقاله روی همین لینک کلیک کنید